Ángulos y rectas que se intersecan (2da parte)
ÁNGULOS ADYACENTES
Dos ángulos adyacentes, contiguos o consecutivos son los que están situados, uno a continuación del otro de manera que un lado es común (el mismo) para los dos ángulos y los otros dos lados pertenecen a una misma recta y la suma de sus ángulos vale 180º:

Estos dos ángulos son contiguos, uno pegado al otro, pero no son adyacentes porque aunque tengan el lado OB común, los otros dos lados no corresponden a la misma recta, y además, la suma de sus ángulos no suman 180º:

Estos ángulos son adyacentes porque tienen el lado OB común a los dos ángulos y los otros dos lados pertenecen a la misma recta y la suma de ambos ángulos equivale al valor del ángulo llano.
ÁNGULOS OPUESTOS POR EL VÉRTICE
Dos ángulos son opuestos por el vértice cuando los lados de uno de ellos son semirrectas de los lados del otro.

Los lados ![]() son las semirrectas de
son las semirrectas de ![]() .
.
En cambio, los lados ![]() no son semirrectas de
no son semirrectas de![]()
ÁNGULOS DETERMINADOS POR RECTAS PARALELAS CORTADAS POR UNA SECANTE
Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:
Las recta r corta a las rectas paralelas m y n:
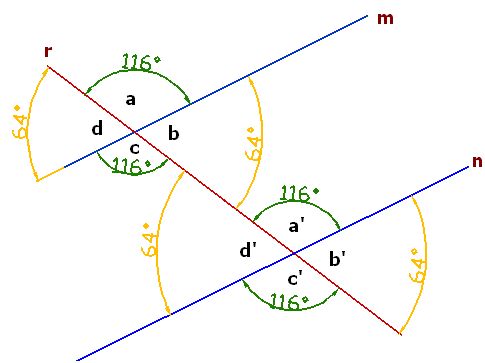
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:
Interiores o internos:
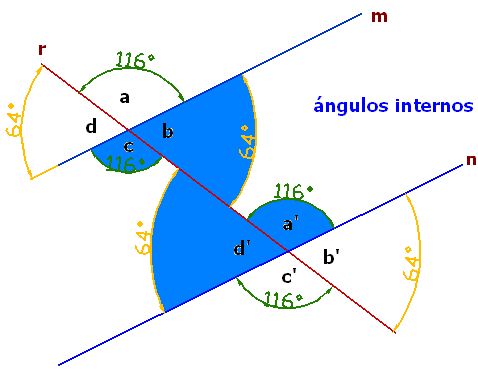
En azul, son los que se encuentran entre las rectas paralelas.
Ángulos exteriores o externos:

Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.
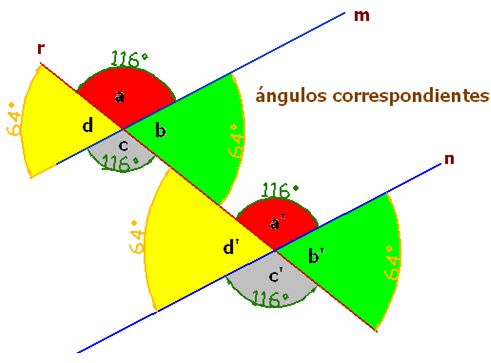
Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Los ángulos del mismo color son correspondientes:
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.
Ángulos alternos internos
Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:
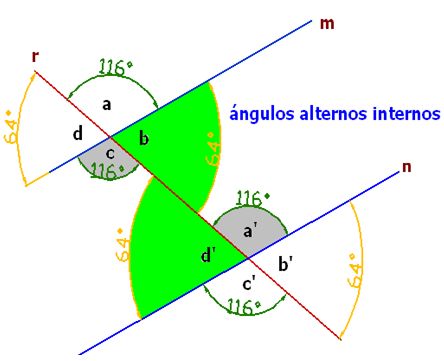
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.
Ángulos alternos externos:
Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:
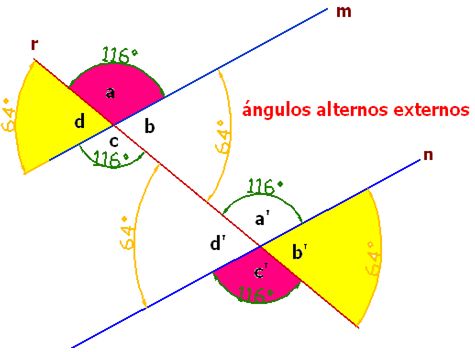
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.



